|
Реферат: Усложнение решающего правила при управлении в задачах распознавания образовРеферат: Усложнение решающего правила при управлении в задачах распознавания образовБекмуратов К.А. Рассматривается один из возможных принципов усложнения решающего правила непрерывного пространства признаков, порождаемого опорными объектами конкретного образа. Предложена процедура нахождения предельного значения размерности признакового пространства, в котором возможно кусочно-линейное разделение образов и гарантированы требуемые качество и надежность распознавания, необходимые в системах управления. В работе [1] описан метод формирования пространства непрерывных признаков, приводящий к безошибочному разделению образов. Введено понятие непрерывного признака и показано, что если набирать пространство только из определенных в [1] признаков, то можно достичь безошибочного разделения образов. В данной работе так же, как и в [2], рассмотрим случай, когда в пространстве непрерывных признаков размерности n безошибочное разделение обучающей последовательности невозможно. Пусть
на некотором множестве Допустим,
что Требуется
с использованием обучающую выборки из
заданных образов Если
обучающая последовательность не может быть безошибочно разделима выбранным
решающим правилом, то в общем случае справедлива теорема Вапника - Червоненкиса
[3], смысл которой состоит в том, что если в n-мерном
пространстве признаков решающее правило совершает
где N- число всевозможных правил заданного класса, которое можно построить в пространстве заданной размерности. Предположим,
что в процессе обучения из последовательно поступивших непрерывных свойств относительно
где
Логарифмируя получим
Если
учесть
где
Подставляя (3) в (2), получаем
Используя теорему Вапника-Червоненкиса [3], можно вычислить предельную размерность пространства
которая
при заданных Пусть
вычислено максимально допустимое значение размерности пространства
Далее,
для того чтобы в процессе обучения синтезировать пространство, в котором
линейное решающее правило (6) безошибочно разделило бы обучающую выборку
Минимально допустимая разделяющая сила признака позволяет при синтезе непрерывного пространства использовать не все признаки, а выбирать только те, разделяющая сила которых удовлетворяет неравенству
Допустим,
что в синтезированном пространстве непрерывных признаков размерности n линейная решающая функция (9) совершает ошибки с частотой
где
N* - соответствует решающему правилу, работающему с
частотой ошибки С использованием этого соотношения, можно установить целесообразность усложнения решающего правила в случае, если в пространстве размерности n ещё не достигнуто безошибочное разделение обучающей выборки. Известно [3], что если вместо линейного правила используется кусочно-линейное и оно безошибочно разделяет обучающую выборку длины l, то в соответствии (7) вместо n следует выбирать величину n=nk+k , (8) где k - число линейных решающих правил, составляющих искомое кусочно - линейное правило. Используя соотношения (7) и (8), ответим на вопрос: стоит ли усложнять решение, если линейное правило в пространстве размерности n не обеспечивает безошибочного разделения обучающей выборки. Для этого нужно сделать подстановку:
В этом случае усложнение решающего правила, определяемое числом k, не приведёт к снижению вероятности ошибки, если будет выполнено соотношение (7) после подстановки (8). Из этого условия можно найти такое значение k, выше которого теряет всякий смысл усложнение решающего правила, действующего в пространстве непрерывных признаков размерности n:
Таким
образом, если выбирать n и k
согласно (5) и (10), то процедура позволяет, при синтезе пространства,
использовать не все признаки, а выбирать только те, разделяющая сила которых
позволяет при заданных Список литературы 1. Бекмуратов. К.А. Процедура формирования непрерывных признаковых пространств при последовательном обучении. Узб. Журнал // «Проблемы информатики и энергетики».- 1994.-№4.-С.17-20. 2. К.А. Бекмуратов. Пошаговая проверка целесообразности усложнения решающего правила при последовательном обучении задаче распознавания. Узб. Журнал // «Проблемы информатики и энергетики». -2000. -№1. – С. 16-19. 3. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов.(Статистические проблемы обучения). – М.: Наука, 1974. –С. 415. |
|
|
| 17.06.2012 |
| Большое обновление Большой Научной Библиотеки |
| 12.06.2012 |
| Конкурс в самом разгаре не пропустите Новости |
| 08.06.2012 |
| Мы проводим опрос, а также небольшой конкурс |
| 05.06.2012 |
| Сена дизайна и структуры сайта научной библиотеки |
| 04.06.2012 |
| Переезд на новый хостинг |
| 30.05.2012 |
| Работа над улучшением структуры сайта научной библиотеки |
| 27.05.2012 |
| Работа над новым дизайном сайта библиотеки |

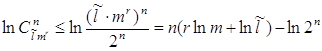 (3)
(3)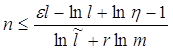 ,
(5)
,
(5)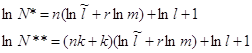 ,
(9)
,
(9)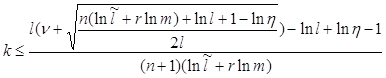 . (10)
. (10)